Verify this identity (tan^2(x)1)/(1tan^2(x)) = 12cos^2(x) ~~~~~ It is done in 3 (three) easy steps 1 The numerator tan^2(x) 1 = = (1) 2 The denominator 1 tan^2(x) = = = (2) 3The Pythagorean identity tells us that no matter what the value of θ is, sin²θcos²θ is equal to 1 We can prove this identity using the Pythagorean theorem in the unit circle with x²y²=1Yes, sec 2 x−1=tan 2 x is an identity sec 2 −1=tan 2 x Let us derive the equation We know the identity sin 2 (x)cos 2 (x)=1 ——(i) Dividing throughout the equation by cos 2 (x) We get sin 2 (x)/cos 2 (x) cos 2 (x)/cos 2 (x) = 1/cos 2 (x) We know that sin 2 (x)/cos 2 (x)= tan 2 (x), and cos 2 (x)/cos 2 (x) = 1 So the equation (i) after substituting becomes

Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby
Tan^2x-1 identity
Tan^2x-1 identity-You can put this solution on YOUR website!Verify the identity {eq}1 \tan^2x = \frac{\cos2x}{\cos^2x} {/eq} Identity An identity is an equation that holds true for any given variable value We have many commonly used trigonometric


How To Prove Csc 2x 1 Tan 2x 1 Is Equivalent To Cosec 2x Quora
= 2 cos2 x – 1 • Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;8/19/16 · (2cos^2x1)(1tan^2x)=1tan^2x Please Help?How to prove the identity (2cos^2x1)(1tan^2x)=1tan^2x Please Help?How to prove the identity This entry was posted in ATVs on August 19, 16 by Asher Burt Post navigation1/8/18 · Explanation This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Confirming that the result is an identity Yes, sec2 − 1 = tan2x is an identity
Identity tan (2x) Multiple Angle Identities Symbolab Identities Pythagorean Angle Sum/Difference Double Angle Multiple Angle Negative Angle Sum to Product Product to SumPeriodicity Identities, radians Periodicity Identities, degrees sin (x 2π) = sin xcsc (x 2π) = csc xsin (x 360°) = sin xcsc (x 360°) = csc xcos (x 2πThe trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is \(Sin 2x = 2 sin x cos x\) Where x is the angle
You have seen quite a few trigonometric identities in the past few pages It is convenient to have a summary of them for reference These identities mostly refer to one angle denoted θ, but there are some that involve two angles, and for those, the two angles are denoted α and β The more important identities6/19/ · Yes, sec2−1=tan2x is an identity Why is cos an even function?Trigonometric Identities ( Math Trig Identities) sin (theta) = a / c csc (theta) = 1 / sin (theta) = c / a cos (theta) = b / c sec (theta) = 1 / cos (theta) = c / b tan (theta) = sin (theta) / cos (theta) = a / b cot (theta) = 1/ tan (theta) = b / a sin (x) = sin (x)



Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction



Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi
3/25/15 · For questions 1 – 5, decide whether the equation is a trigonometric identity Explain your reasoning cos2 x(1 tan2 x) = 1 sec x tan x(1 – sin2 x) = sin x csc x(2sin x √2) = 0 cos2(2x) – sin2(2x) = 0 sin2 θ csc2 θ = sin2 θ cos2 θTan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan(2x) = 2 tan(x) / (1 · How to prove the trigonometry equation is an identity?



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



Derive 1 Tan 2x Sec 2x And 1 Cot 2x Text Cosec 2x Geometrically Mathematics Stack Exchange
Verify the Identity tan(2x)^2sin(2x)^2cos(2x)^2=sec(2x)^2 Start on the left side Apply Pythagorean identity Tap for more steps Apply pythagorean identity Apply pythagorean identity Because the two sides have been shown to be equivalent, the equation is an identity is an identity1 cos A But sinA cosA =tanA and 1 cosA =secA (Notethat thedefinitionofthesecantofA is 1 cosA) Hence tan2 A1=sec2 A Thisisanotherimportantidentity Key Point tan2 A1=sec2 A Onceagain,returningto sin 2Acos A =1 wecandividethroughbysin2 A togive sin2 A sin 2A cos2 A sin A = 1 sin2 A But cosA sinA =cotA and 1 sinA =cosecASimplify trigonometric expressions Calculator online with solution and steps Detailed step by step solutions to your Simplify trigonometric expressions problems online with our math solver and calculator Solved exercises of Simplify trigonometric expressions
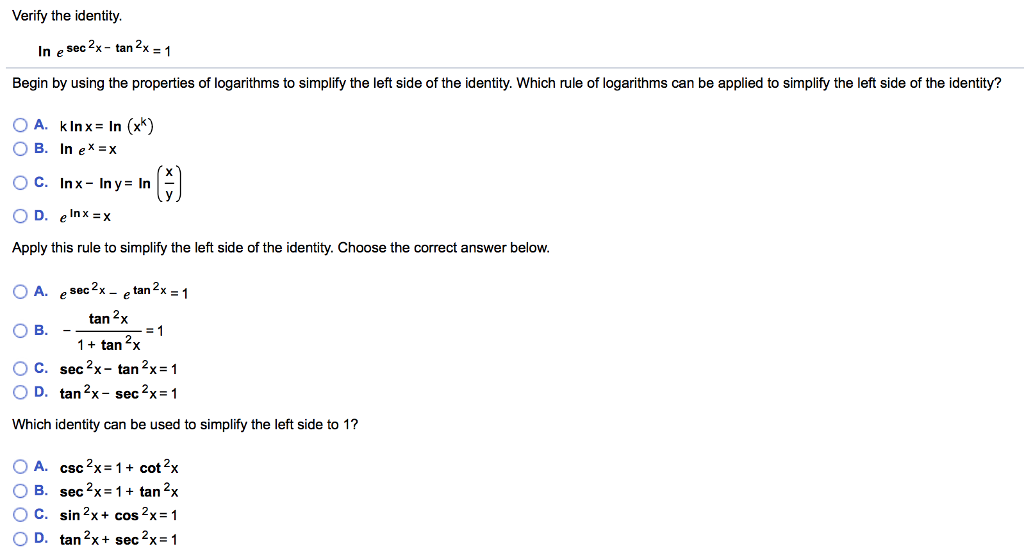


Solved Verify The Identity In Esec 2x Tan 2x 1 Begin By Chegg Com



1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube
Siyavula's open Mathematics Grade 12 textbook, chapter 4 on Trigonometry covering Double angle identities$$2\cot4x = \cot2x \tan2x$$ Thank you in advance Thank you for the comments and hints I got an answer after many tries ;) Below is my answer Thank you $2cot4x = cot2x tan2x$ $2\frac{1}{tan 4x} = cot2x tan2x$ $2\frac{1}{\frac{2 tan 2x}{1 tan^2 2x}} = cot2x tan2x$X) 2 1 = 1 cos 2 x There aren't any terms or factors involving in this formula, so let's make up another one An equivalent formula for is math\implies\tan^2x=\dfrac {\sin^2x\sin^2x\cos^2x} {\sin /math Continue Reading


Tan2x ただの悪魔の画像



Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity
Equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4 cot x = 1/tan x equation 5 sin 2 x cos 2 x = 1 equation 6 tan 2 x 1 = sec 2 x equation 7 1 cot 2 x = csc 2 x equation 8 cos (x y) = cos x cos y sin x sin y equation 9 sin (x y) = sin x cos y cos x sin y equation 10 cos (x) = cos x equation 11 cos (pi/2 x) = sin x equation 12=> `1 2*tan^2x` It is seen that `sec^4 x tan^4 x = 1 tan^2 x` is not an identity, instead `sec^4x tan^4x = 1 2*tan^2x` Approved by eNotes Editorial Team2 x I started this by making sec 1/cos and using the double angle identity for that and it didn't work at all in any way ever Not sure why I can't do that, but something was wrong Anyways I looked at the solutions manual and they magic out 1 tan x tan 2 x = 1 tan



3 Simplifying Trig Expression 1 Tan 2x Youtube



Ln Sec 5 3 Key Pdf Ln 5 3 1 Verify The Identity A Math 1730 Name Key Sin 2 X 2sin X Cos X Cos 2 X Tan 2x 1 Cos 2
10/26/11 · The identity `tan^2 x = (1 cos(2x))/(1 cos(2x))` has to be proved Find sin 2x, cos 2x, and tan 2x from the given informationFind sin 2x, cos 2x, and tan 2x\(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomes \(tan(aa) =\frac{ tan a tan a }{1 tan a tana}\) \(Tan 2a =\frac{2tan a}{1tan^{2}a} \) Practice Example for tan 2 theta Question Find tan 2 x, if tan x = 5 Solution · In this section we look at how to integrate a variety of products of trigonometric functions These integrals are called trigonometric integralsThey are an important part of the integration technique called trigonometric substitution, which is featured in Trigonometric SubstitutionThis technique allows us to convert algebraic expressions that we may not be able


Prove Sin2x 2tanx 1 Tan 2x Socratic



Tan 2x Identity Learn Lif Co Id
5/29/16 · The identity $$\frac{\tan(2x)\tan(3x)}{1\tan(2x)\tan(3x)}$$ Stack Exchange Network Stack Exchange network consists of 177 Q&A communities including Stack Overflow , the largest, most trusted online community for developersProving Trigonometric Identities Calculator online with solution and steps Detailed step by step solutions to your Proving Trigonometric Identities problems online with our math solver and calculator Solved exercises of Proving Trigonometric IdentitiesThe cosine is an even function which means that if (x,y) is on the graph of the function so too is the point (x,y)



Tangent Half Angle Formula Wikipedia



9 1 Identities And Proofs Ppt Download
Rewrite 1 cos(x)sin(x) 1 cos ( x) sin ( x) as 1 sin(x)cos(x) 1 sin ( x) cos ( x) 1 sin(x)cos(x) 1 sin ( x) cos ( x) Because the two sides have been shown to be equivalent, the equation is an identity 1 tan(x) tan(x) = 1 sin(x)cos(x) 1 tan ( x) tan ( x) = 1 sin ( x) cos ( x) is an identityA follow up proof to accompany sin^2 cos^2 =1 Another identity that is used quite a bit, especially in calculus involving trigonometric functionsDecide whether the equation is a trigonometric identity explain your reasoning cos^2x(1tan^2x)=1 secxtanx(1sin^2x)=sinx cos^2(2x)sin^2=0 ** cos^2x(1tan^2x)=1 cos^2xsin^2x/cos^2x=1 cos^2xsin^2x=1 left side = right side, therefore, equation is an identity secxtanx(1sin^2x)=sinx (1/cosx*sinx/cosx)(11cos^2x (sinx/cos^2x)(cos^2x)=sinx



Trig Identity Sec2x Minus Tan2x T10 Youtube



F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2
· Explanation Change to sines and cosines then simplify 1 tan2x = 1 sin2x cos2x = cos2x sin2x cos2x but cos2x sin2x = 1 we have ∴ 1 tan2x = 1 cos2x = sec2x Answer linkProve\\cot (2x)=\frac {1\tan^2 (x)} {2\tan (x)} prove\\csc (2x)=\frac {\sec (x)} {2\sin (x)} prove\\frac {\sin (3x)\sin (7x)} {\cos (3x)\cos (7x)}=\cot (2x) prove\\frac {\csc (\theta)\cot (\theta)} {\tan (\theta)\sin (\theta)}=\cot (\theta)\csc (\theta) prove\\cot (x)\tan (x)=\sec (x)\csc (x) trigonometricidentityprovingcalculator enTanx = t Sec^2 x dx= dt So now it is, 1/(1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx Integral of the function \frac{\cos ^2 x}{1\tan x} Integral of the function 1



Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities
Tan(2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin(2x) to cos(2x) sin(2 x ) = 2 sin( x ) cos( x ) cos(2 x ) = (cos( x ))^2 – (sin( x ))^2 = 1 – 2 (sin( x ))^2 = 2 (cos( x ))^2 – 1In the first method, we used the identity sec 2 θ = tan 2 θ 1 sec 2 θ = tan 2 θ 1 and continued to simplify In the second method, we split the fraction, putting both terms in the numerator over the common denominator This problem illustrates that there are multiple ways we can verify an identity Employing some creativity canPythagorean identities are identities in trigonometry that are extensions of the Pythagorean theorem The fundamental identity states that for any angle θ, \theta, θ, cos 2 θ sin 2 θ = 1 \cos^2\theta\sin^2\theta=1 cos2 θsin2 θ = 1



How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic


5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download
Pythagorean identities Main article Pythagorean trigonometric identity In trigonometry, the basic relationship between the sine and the cosine is given by the Pythagorean identity sin 2 θ cos 2 θ = 1 , {\displaystyle \sin ^ {2}\theta \cos ^ {2}\theta =1,}In trigonometry formulas, we will learn all the basic formulas based on trigonometry ratios (sin,cos, tan) and identities as per Class 10, 11 and 12 syllabi Also, find the downloadable PDF of trigonometric formulas at BYJU'SCos 2x ≠ 2 cos x;



Verify Each Trigonometric Equation By Substituting Identities To Match The Right Hand Side Of The Brainly Com



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
11/27/15 · One answer is to say that, properly, the identity is $\sec^2x=1\tan^2x$, where the sides fail to be defined at the same values Share Improve this answer Follow edited Nov 27 '15 at 2246 Joel Reyes Noche 9,278 2 2 gold badges 28 28 silver badges 70 70 bronze badgesSubstitute the trigonometric identity `tan^2(x) = sec^2(x)1` Note This is the same as `1 tan^2(x) = sec^2(x)` `(tan^2(x))/(1tan^2(x)) = (sec^2(x)1)/(sec^2(x))`PROVE THE IDENTITY (1tan^2x)/ (1tan^2x ) = 12sin^2x IN URDU / HINDI SUMMER 07 PAPER 1 QUESTION 3 SUMMER 07 PAPER 1 QUESTION 3 AboutPressCopyrightContact



Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby



How Do You Prove Tan 2x Secx 1 1 Secx Socratic
Trigonometry Verify the Identity (1sin (x)^2) (1tan (x)^2)=1 (1 − sin2 (x))(1 tan2 (x)) = 1 ( 1 sin 2 ( x)) ( 1 tan 2 ( x)) = 1 Start on the left side (1−sin2 (x))(1tan2 (x)) ( 1 sin 2 ( x)) ( 1 tan 2 ( x)) Apply Pythagorean identity Tap for more steps Apply pythagorean identityThe half‐angle identity for tangent can be written in three different forms In the first form, the sign is determined by the quadrant in which the angle α/2 is located Example 5 Verify the identity Example 6 Verify the identity tan (α/2) = (1 − cos α)/sin α Example 7 Verify the identity tan (α − 2) = sin π/(1 cos α)Prove the identity (1tanx)^2 (1 cotx)^2 is equivalent to (secx cosecx)^2 Identities tan^21=sec^2 cot^21=csc^2 Start with left side



How Do You Prove Tan 2x Secx 1 1 Secx Socratic



1 Cosx 1 Cosx Tan 2x Secx 1 2prove Brainly In



Find Sin 2x Cos 2x And Tan 2x If Tan X 1 2 And X Terminates In Quadrant Iii Helpyout



Solved 2 Prove The Following Trig Identities A Prove Chegg Com


7 Proving Ids Trig Functions Identities



How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic



Integrate Tan 2x



Using Trigonometric Identities Video Khan Academy



Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco



Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube


How To Prove Math Dfrac Sqrt 1 Cos 2x 1 Cos 2x Tan X Math Quora


Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec


Tan 2x Sec 2x Youtube
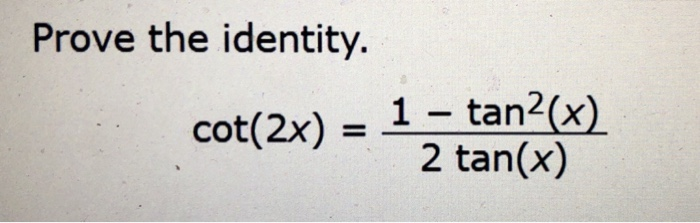


Solved Prove The Identity Cot 2x 1 Tan2 X 2 Tan X Chegg Com



Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube


Prove That Cos2x Cos 2x Sin 2x 2cos 2x 1 1 2sin 2x 1 Tan 2x 1 Tan 2x Sarthaks Econnect Largest Online Education Community


A Trig Identity
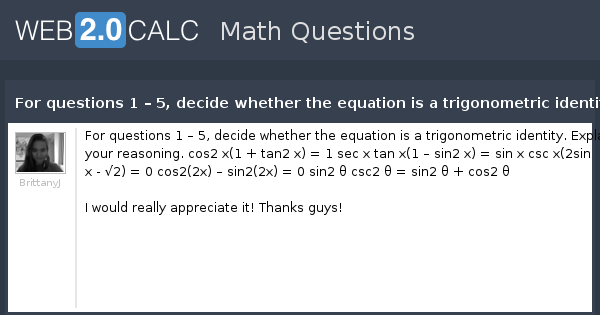


View Question For Questions 1 5 Decide Whether The Equation Is A Trigonometric Identity Explain Your Reasoning



Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com



Trig Identities Bingo Card
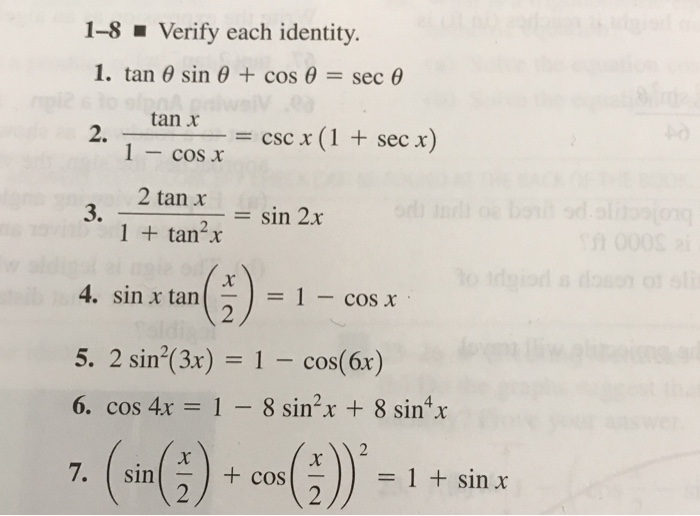


Solved 1 8 Verify Each Identity Sec 8 1 Tan 8 Sin 8 Chegg Com
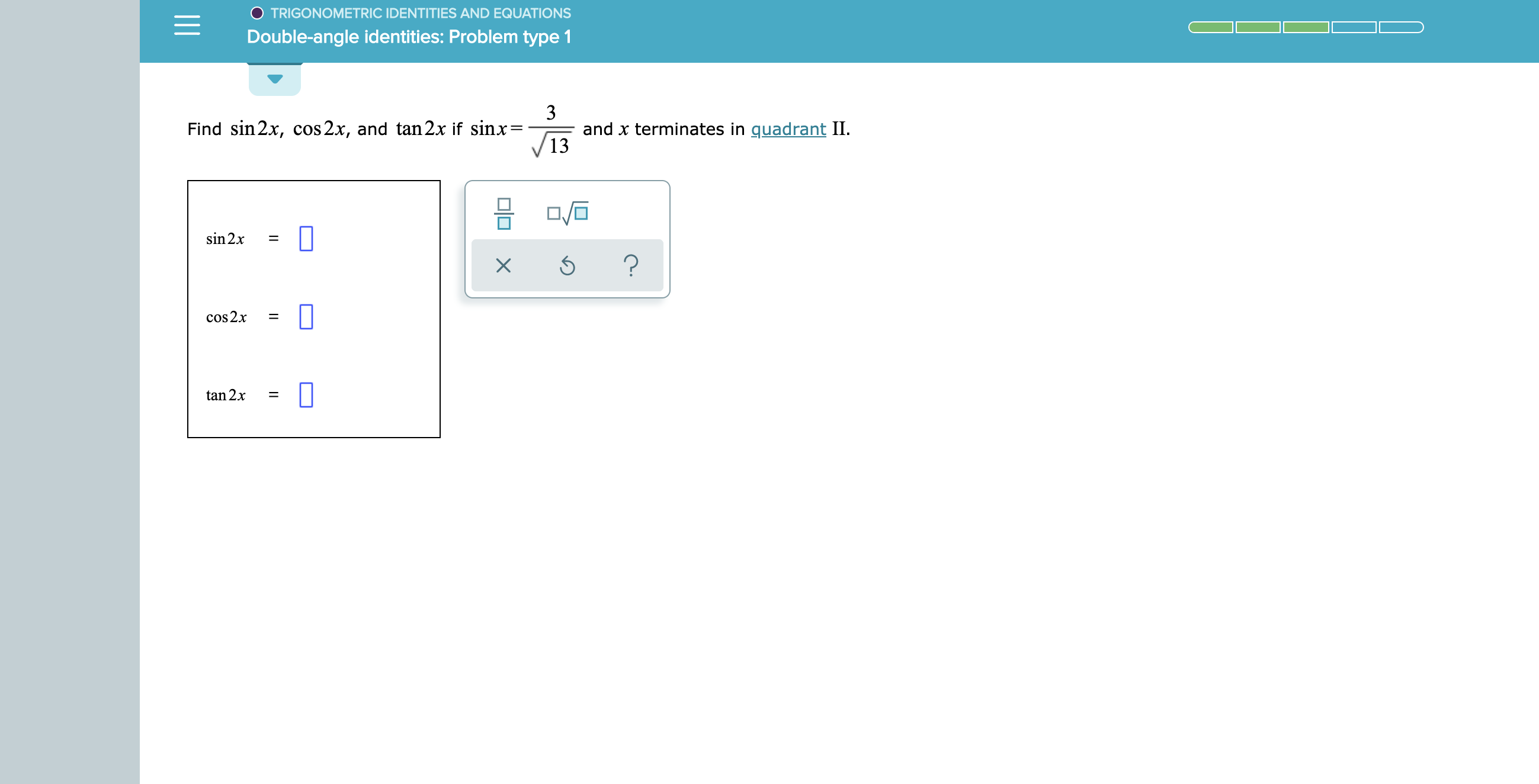


Answered Trigonometric Identities And Equations Bartleby


What Is The Formula Of Tan2x Quora



Tan 2x Identity Learn Lif Co Id


Solution Tan 2x Secx 1 1 Cosx Cosx Please And Thank You
x-1=sec(squared)x.jpg)


10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com


How To Prove Csc 2x 1 Tan 2x 1 Is Equivalent To Cosec 2x Quora



Solved Prove The Identity 1 Tan X Tan Y Cos X Y Chegg Com



Trigonometry Reciprocal Identities Expii


Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero
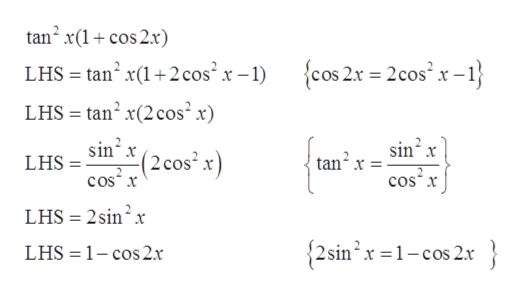


Answered Tan2x 1 Cos2x 1 Cos2x Verify The Bartleby


True Or False The Equation Sec 2 X 1 Tan 2 X Is An Identity Brainly Com


How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora
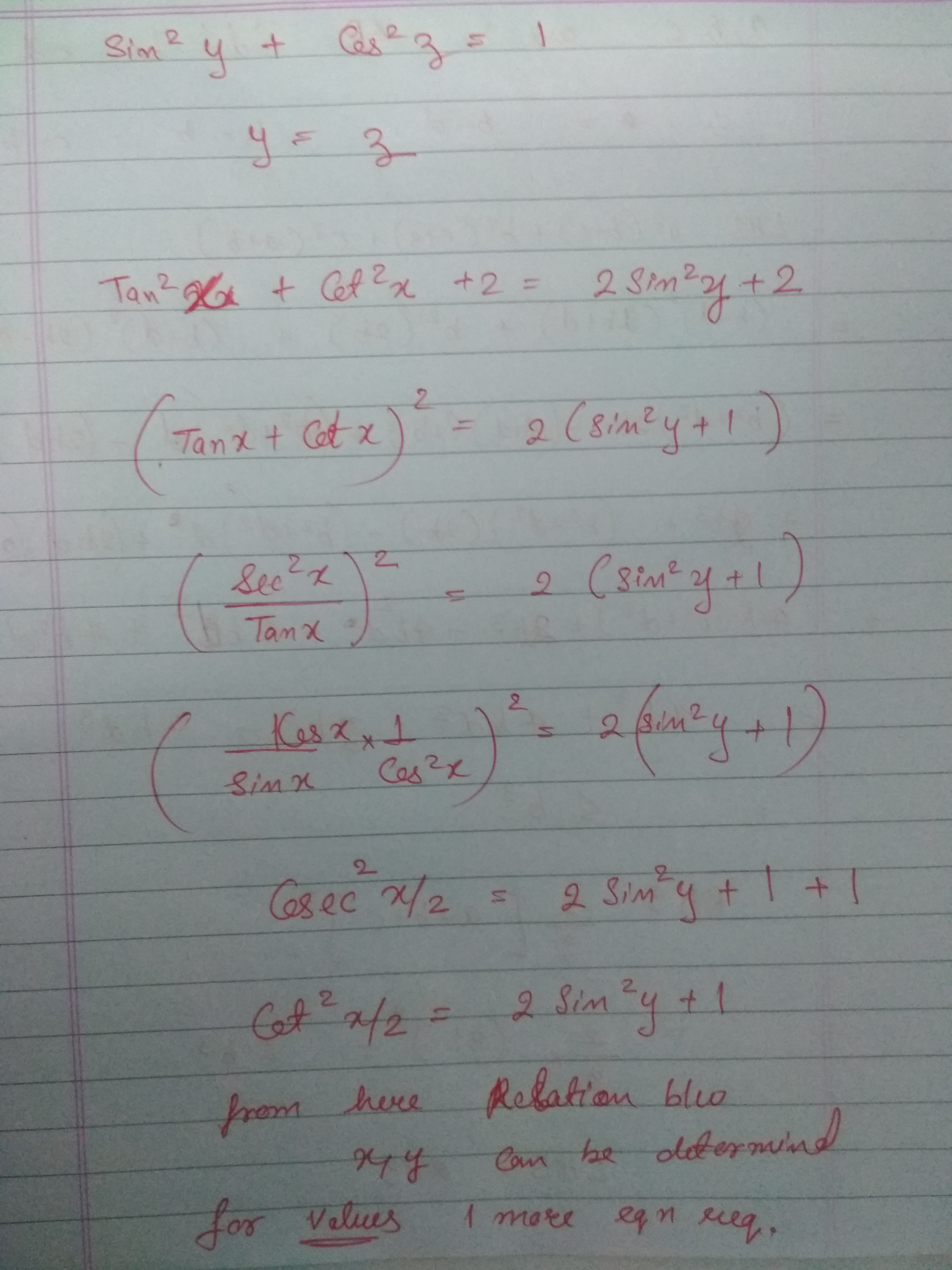


Solve For X Y And Z If Tan 2x Cot 2x 2sin 2y And Sin 2y Cos 2z 1 Askiitians



Solved Evaluate Integral Tan 6 2x Sec 4 2x Dx If We Chegg Com



Integrate Sec 2x Method 1



Proof Tan 2 1 Sec 2 Youtube



Double Angle Identities Solutions Examples Videos Worksheets Games Activities



Ch Ppt Download



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo


What Is The Formula Of Tan2x Quora


Ilectureonline



1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube



Solved Verify The Identity 4 2 Tan X Secx2tan X 1 Whic Chegg Com



Sec22x 1 Tan 2x Find The General Solution Maths Trigonometric Functions Meritnation Com



How To Use Trig Identities Mathematics Stack Exchange



How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic
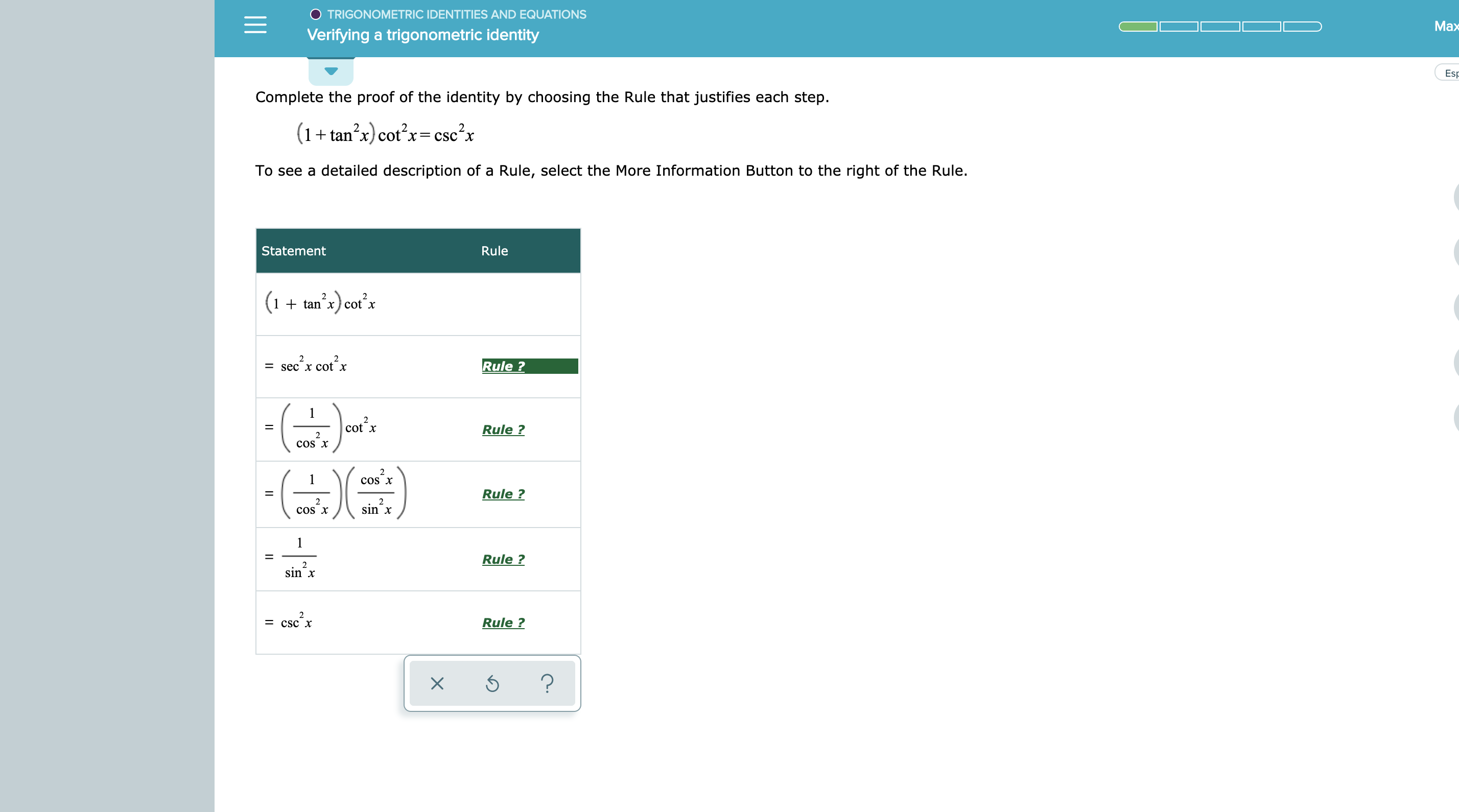


Answered Trigonometric Identities And Equations Bartleby



Which Of The Following Is Not An Identity A Cosx Sinx 2 1 2cosx Sinx B 1 Cos 2x Sin 2 1 Brainly Com



Solved Verify The Identity 2 X Tan 2 X Esec X Tan X Sec Chegg Com



2sinxcosx Identity Gamers Smart



Chapter 11 Trigonometric Identities And Equations 11 1



Tan 2x 1 Sec 2x Tan X



Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube


Biomath Trigonometric Functions
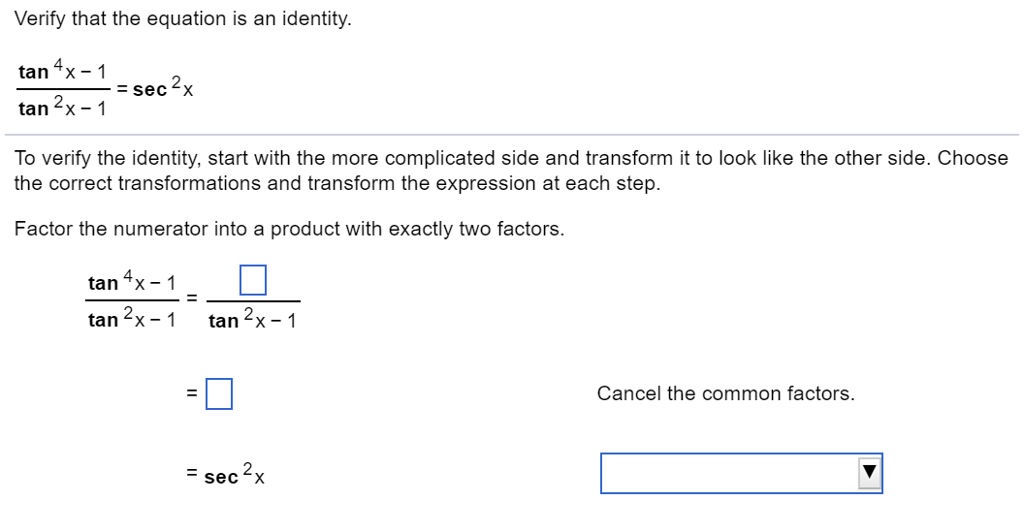


Solved Verify That The Equation Is An Identity Tan 4x 1 Chegg Com



Double Angle And Half Angle Identities Example Sin 28 Cos 2a Or Tan 2x



Trig Double Identities Trigonometric Double Angle Functions Trig


Solution Verify The Identity By Showing That The Left Equals Right Sec 2x 1 Tan 2 Sec2x Do I Use 1 Cos 2x 1 Tan 2x Or Do I Use 1 Tan 2x 1 Tan 2x Either Way I Do Not Know Where To Go Fro


Trig Identities Hsn Forum


View Question Trigonometric Identities



Trig Identities And Formulas Pre Calculus Quiz Quizizz



How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic



How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic


Trig Identities Hsn Forum



Tangent Half Angle Formula Wikipedia



Tan2x ただの悪魔の画像



5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download



0 件のコメント:
コメントを投稿